Задача 1.
а) Дадени са изразите:
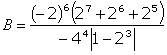
Да се представи А с многочлен в нормален вид.
Да се намери числото, равно на стойността на В.
Да се реши неравенството A > B и да се намерят стойностите на a, за които това неравенство и неравенството x > a имат точно едно общо цяло решение.
б) Двама работници
получили за извършена работа 1050 лева. Първият работил 25 дни, а вторият
- с 20% по-малко дни.
По колко лева дневно е заработвал всеки от работниците, ако първият за
5 дни получил 10 лева повече, отколкото вторият - за 4 дни?
Задача 2.
Даден е ромб АВСD.
а) Точките
M и
N са
съответно от страните AB
и BC
на ромба и са такива, че AM
+ CN
= CD.
Да се намерят мерките на ъглите на ромба, ако триъгълникът с върхове М,
B и
D и триъгълникът с върхове N,
C и
D са еднакви.
б) Нека ![]() CAD
:
CAD
: ![]() ABD
= 1 : 2. Построени са височината BH
(H
ABD
= 1 : 2. Построени са височината BH
(H![]() CD)
на ромба и точка Р
от лъча
CD)
на ромба и точка Р
от лъча ![]() ,
такава че DP
= 4DH.
,
такава че DP
= 4DH.
Да се докаже, че правите PC
и BH
са успоредни и че периметърът на ![]() DTP
е по-малък от периметъра на
DTP
е по-малък от периметъра на ![]() DOP,
където Т
е пресечната точка на АС
и BP,
а О
е пресечната точка на диагоналите на ромба.
DOP,
където Т
е пресечната точка на АС
и BP,
а О
е пресечната точка на диагоналите на ромба.
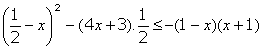
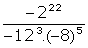 е негово решение.
е негово решение.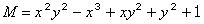 ,
,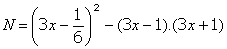 и
и 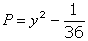 .
.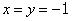 .
.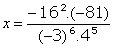 .
. 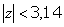 .
. 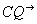 е ъглополовящата на
е ъглополовящата на