Задача 1.
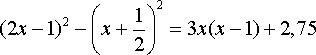
и да се намерят стойностите на параметъра a, за които корените на уравнението |3a - 2x| = 2 са решения на неравенството.
Оригиналният текст и кратки решения на темата са публикувани на 25.06.2001г. от МОН
|
Задача 1. |
| Да се реши: |
а) уравнението 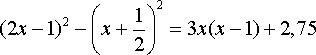 |
| б) неравенството |
|
| Задача 2. |
| Диагоналите на ромба АВСD, в
който |
| а) Ъглополовящата на |
| б) Височината DE (Е |
ОТГОВОРИ |
|
Задача 1.а) x = -1 б) Задача 2.а)
|
|
| РЕШЕНИЯ |
|
| Разработката ни е с цел да се изчисли електронно оценката. Отбележете в кутията вляво ако сте извършили съответните действия. Изчислената оценка може да видите в края на страницата. | |
Задача 1.
|
|
|
|
||
|
©Copyright 2001г. А. M. S.
All rights reserved..
|